Projects

This page describes some of the projects that our group has worked on. The full details of these projects can be found in our group's publications, presentations, posters, and theses.

Transform Learning Involving CG (ICIP 2012, TSP 2013)

The sparsity of signals and images in a certain transform domain or dictionary has been exploited in many applications in signal and image processing. Analytical sparsifying transforms such as Wavelets and DCT have been widely used in compression standards. Recently, synthesis sparsifying dictionaries that are directly adapted to the data have become popular especially in applications such as image denoising, inpainting, and medical image reconstruction. While there has been extensive research on learning synthesis dictionaries and some recent work on learning analysis dictionaries, the idea of learning sparsifying transforms has received no attention. In this work, we propose novel problem formulations for learning sparsifying transforms from data. The proposed alternating minimization algorithms give rise to well-conditioned square transforms. We show the superiority of our approach over analytical sparsifying transforms such as the DCT for signal and image representation. We also show promising performance in signal denoising using the learnt sparsifying transforms. The proposed approach is much faster than previous approaches involving learnt synthesis, or analysis dictionaries.

Doubly Sparse Transform Learning (ICIP 2012, TIP 2013)

Following up on recent work, where we introduced the idea of learning square sparsifying transforms, we propose here novel problem formulations for learning doubly sparse transforms for signals or image patches. These transforms are a product of a fixed, fast analytic transform such as the DCT, and an adaptive matrix constrained to be sparse. Such transforms can be learnt, stored, and implemented efficiently. We show the superior promise of such learnt transforms as compared to analytical sparsifying transforms such as the DCT for image representation. We also show promising performance in image denoising, which compares favorably with approaches involving learnt synthesis dictionaries such as the K-SVD algorithm. The proposed approach is also much faster than K-SVD denoising.

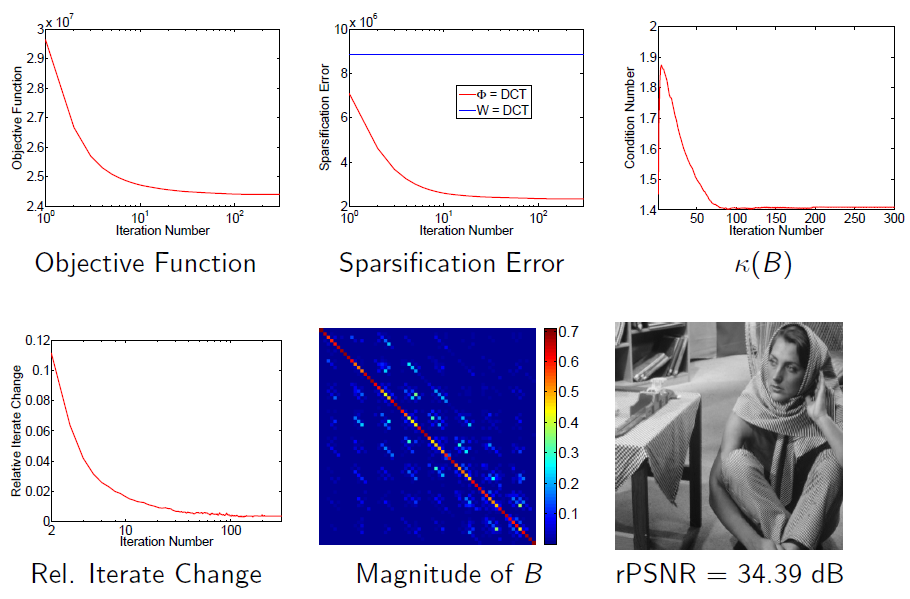
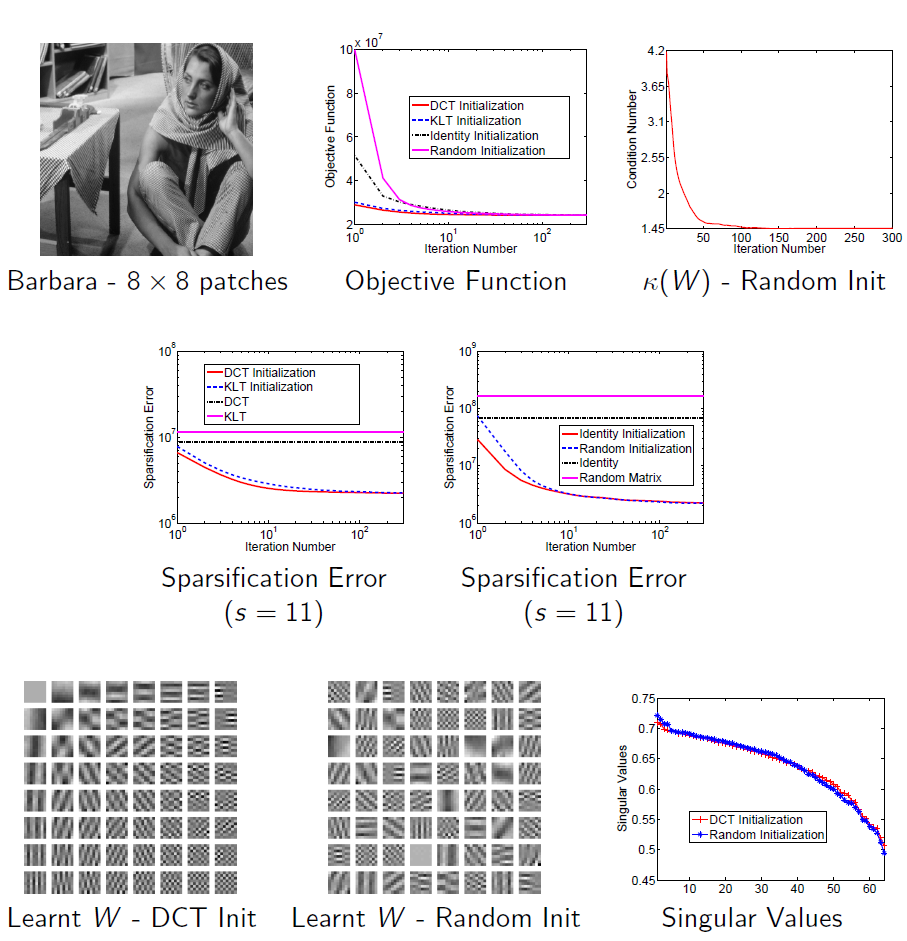
Transform Learning with Closed-form Solutions (ICASSP & SPARS 2013, TSP 2015)

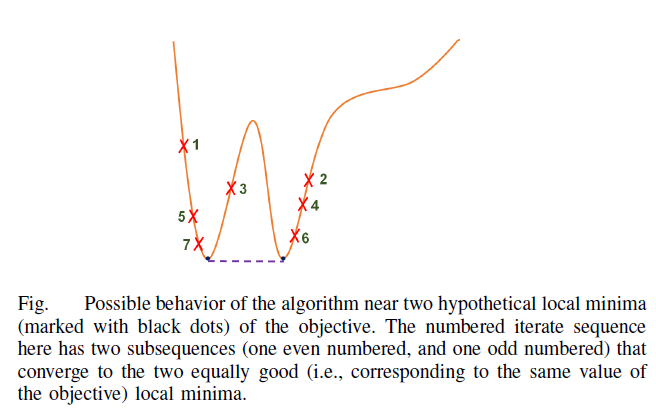
In this work, we focus on the sparsifying transform model, and study the learning of well-conditioned square sparsifying transforms. The proposed algorithms alternate between a l0 norm-based sparse coding step, and a non-convex transform update step. We derive the exact analytical solution for each of these steps. The proposed solution for the transform update step achieves the global minimum in that step, and also provides speedups over iterative solutions involving conjugate gradients. We establish that our alternating algorithms are globally convergent to the set of local minimizers of the non-convex transform learning problems. In practice, the algorithms are insensitive to initialization. We present results illustrating the promising performance and significant speed-ups of transform learning over synthesis K-SVD in image denoising.

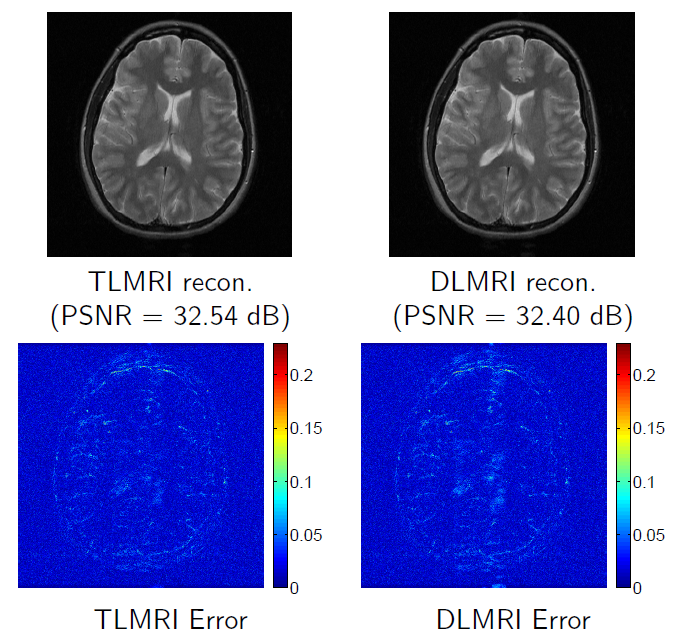
Square Transform Learning for Compressed Sensing MRI (ISBI 2013)

Compressed Sensing (CS) enables magnetic resonance imaging (MRI) at high undersampling by exploiting the sparsity of MR images in a certain transform domain or dictionary. Recent approaches adapt such dictionaries to data. While adaptive synthesis dictionaries have shown promise in CS based MRI, the idea of learning sparsifying transforms has not received much attention. In this work, we propose a novel framework for MR image reconstruction that simultaneously adapts a transform and reconstructs the image from highly undersampled k-space measurements. The proposed approach is significantly faster (>10x) than previous approaches involving synthesis dictionaries, while also providing comparable or better reconstruction quality. This makes it more amenable for adoption for clinical use.

Overcomplete Transform Learning (ICASSP 2013, SPARS 2013)

In this work, we focus on the sparsifying transform model, for which sparse coding is cheap and exact, and study the learning of tall or overcomplete sparsifying transforms from data. We propose various penalties that control the sparsifying ability, condition number, and incoherence of the learnt transforms. Our alternating algorithm for transform learning converges empirically, and significantly improves the quality of the learnt transform over the iterations. We present examples demonstrating the promising performance of adaptive overcomplete transforms over adaptive overcomplete synthesis dictionaries learnt using K-SVD, in the application of image denoising.

Structured OCTOBOS Learning (ICIP 2014, IJCV 2015)

In recent years, there has been growing interest in sparse signal modeling especially using the sparsifying transform model, for which sparse coding is cheap. However, natural images typically contain diverse features or textures that cannot be sparsified well by a single transform. Hence, in this work, we propose a union of sparsifying transforms model. Sparse coding in this model reduces to a form of clustering. The proposed model is also equivalent to a structured overcomplete sparsifying transform model with block cosparsity, dubbed OCTOBOS. The alternating algorithm introduced for learning such transforms involves simple closed-form solutions. A theoretical analysis provides a convergence guarantee for this algorithm. It is shown to be globally convergent to the set of partial minimizers of the non-convex learning problem. We also show that under certain conditions, the algorithm converges to the set of stationary points of the overall objective. When applied to images, the algorithm learns a collection of well-conditioned square transforms, and a good clustering of patches or textures. The resulting sparse representations for the images are much better than those obtained with a single learned transform, or with analytical transforms. We show the promising performance of the proposed approach in image denoising, which compares quite favorably with approaches involving a single learned square transform or an overcomplete synthesis dictionary, or gaussian mixture models. The proposed denoising method is also faster than the synthesis dictionary-based approach.

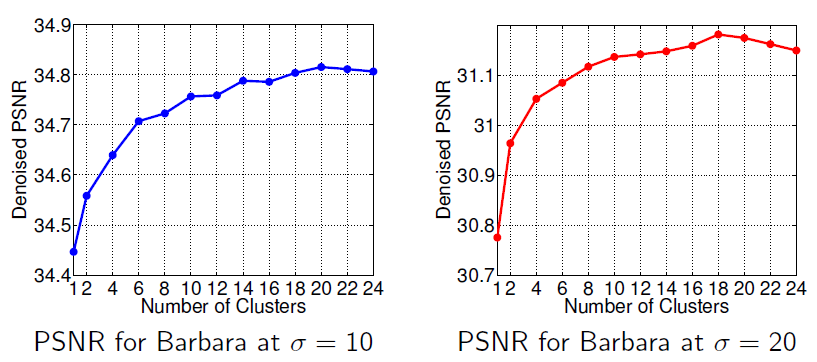
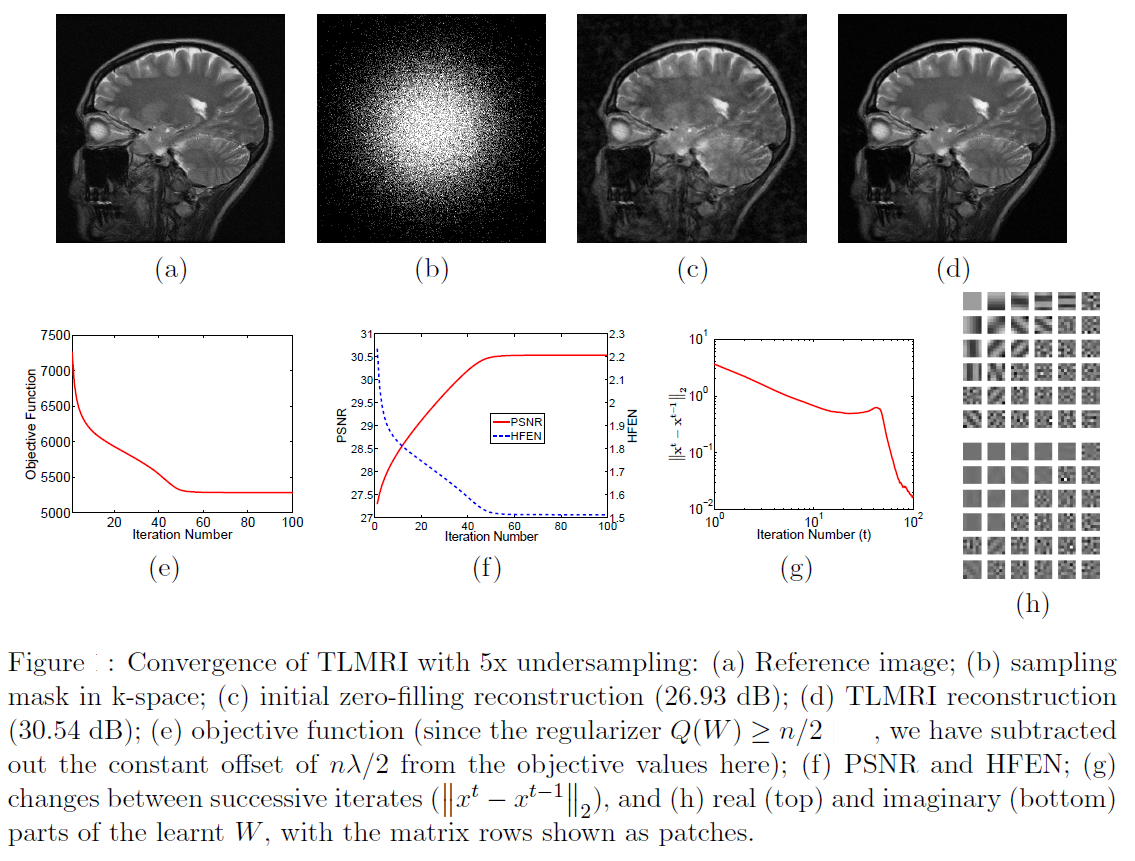
Transform-Blind Compressed Sensing (SIIMS 2015, SAMPTA 2015)

Compressed sensing exploits the sparsity of images or image patches in a transform domain or synthesis dictionary to reconstruct images from undersampled measurements. In this work, we focus on blind compressed sensing, where the underlying sparsifying transform is a priori unknown, and propose a framework to simultaneously reconstruct the underlying image as well as the sparsifying transform from highly undersampled measurements. The proposed block coordinate descent type algorithms involve highly efficient optimal updates. Importantly, we prove that although the proposed blind compressed sensing formulations are highly nonconvex, our algorithms are globally convergent (i.e., they converge from any initialization) to the set of critical points of the objectives defining the formulations. These critical points are guaranteed to be at least partial global and partial local minimizers. The exact point(s) of convergence may depend on initialization. We illustrate the usefulness of the proposed framework for magnetic resonance image reconstruction from highly undersampled k-space measurements. As compared to previous methods involving the synthesis dictionary model, our approach is much faster, while also providing promising reconstruction quality.

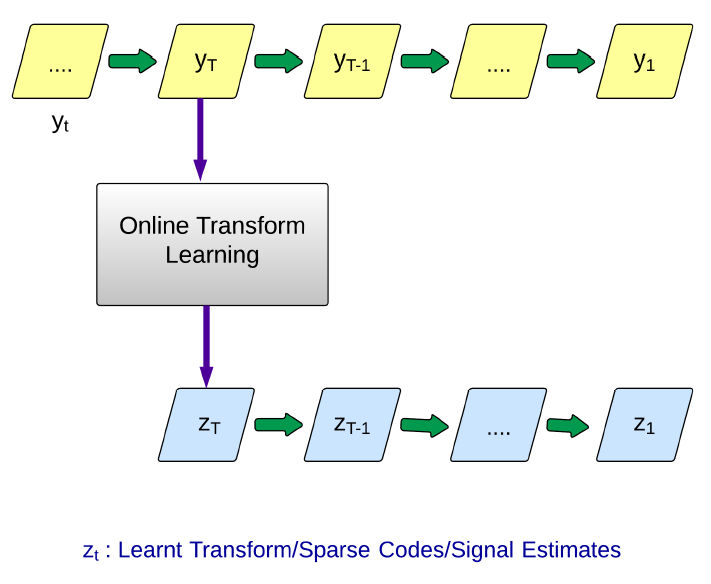
Online Sparsifying Transform Learning (GlobalSIP 2014, JSTSP 2015)

In this work, we develop a methodology for online learning of square sparsifying transforms. Such online learning can be particularly useful when dealing with big data, and for signal processing applications such as real-time sparse representation and denoising. The proposed transform learning algorithms are shown to have a much lower computational cost than online synthesis dictionary learning. In practice, the sequential learning of a sparsifying transform typically converges faster than batch mode transform learning. Preliminary experiments show the usefulness of the proposed schemes for sparse representation, and denoising. We also prove that although the associated optimization problems are non-convex, our online transform learning algorithms are guaranteed to converge to the set of stationary points of the expected (statistical) transform learning cost. The guarantee relies on a few simple assumptions.

Convex Methods for Transform Learning (ICASSP 2014 & Chapter 9 of Ravishankar's Thesis)

Recent works introduced the idea of learning sparsifying transforms from data, and demonstrated the usefulness of learned transforms in image representation, and denoising. However, the learning formulations were non-convex, and the algorithms lacked strong convergence properties. In this work, we propose a novel convex formulation for doubly sparse square transform learning. The proposed formulation has similarities to traditional least squares optimization with l1 regularization. Our convex learning algorithm is a modification of FISTA, and is guaranteed to converge to a global optimum, and moreover converges quickly. We also study two non-convex variants of the proposed convex formulation, and provide a local convergence proof for the algorithm for one of them. These proposed non-convex variants use the l0 norm for measuring the sparsity of the transform and/or sparse code. We show the superior promise of our learned transforms here as compared to analytical sparsifying transforms such as the DCT for image representation. The performance is often comparable to the previously proposed non-convex (non-guaranteed) doubly sparse transform learning schemes.

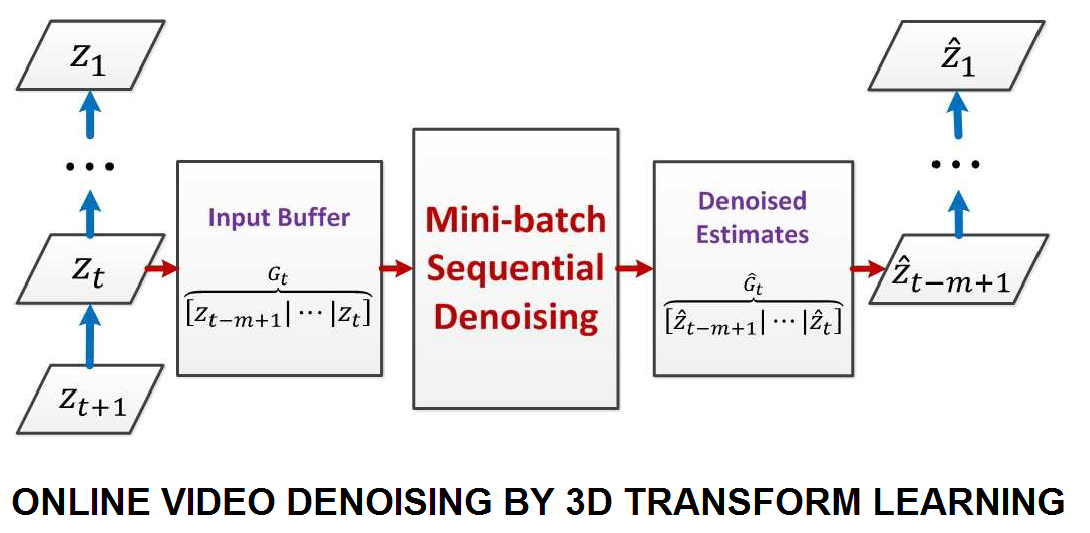
Transform Learning for Video Denoising (ICIP 2015)

Very recently, we proposed methods for online sparsifying transform learning, which are particularly useful for processing large-scale or streaming data. Online transform learning has good convergence guarantees and enjoys a much lower computational cost than online synthesis dictionary learning. In this work, we present a video denoising framework based on online 3D spatio-temporal sparsifying transform learning. The proposed scheme has low computational and memory costs, and can potentially handle streaming video. Our numerical experiments show promising performance for the proposed video denoising method compared to popular prior or state-of-the-art methods.

Filterbank Transform Learning (SPIE 2015)

Data following the transform model is approximately sparsified when acted on by a linear operator called a sparsifying transform. While existing transform learning algorithms can learn a transform for any vectorized data, they are most often used to learn a model for overlapping image patches. However, these approaches do not exploit the redundant nature of this data and scale poorly with the dimensionality of the data and size of patches. We propose a new sparsifying transform learning framework where the transform acts on entire images rather than on patches. We illustrate the connection between existing patch-based transform learning approaches and the theory of block transforms, then develop a new transform learning framework where the transforms have the structure of an undecimated filter bank with short filters. Unlike previous work on transform learning, the filter length can be chosen independently of the number of filter bank channels. We apply our framework to accelerating magnetic resonance imaging. We simultaneously learn a sparsifying filter bank while reconstructing an image from undersampled Fourier measurements. Numerical experiments show our new model yields higher quality images than previous patch-based sparsifying transform approaches.